This is an assignment questions to create a turing machine that perform a simple task, multiplication, factorial, n xn and ackerman function given an input. I am not going to give a lecture on what is universal turing machine and how my simulator work but this should gives people an idea on how you can build a simple universal turing machine and other simulator easily.
Universal Turing Machine
My universal turing machine is some how "cheap". It basically read a string and moves according to how the simulator has instructed it to do. Here is the code of my universal turing machine in Java(J2SE).
public String UTM(String input, String[][] simulator){
int pointer = 0;
int state = 0;
boolean stop = false;
while(true){
String[] tmp = input.split("(?!^)");
for(int i = 0; i < simulator.length;i++){
if(simulator[i][1].equalsIgnoreCase(tmp[pointer]) && simulator[i][0].equalsIgnoreCase(String.valueOf(state))){
tmp[pointer] = simulator[i][2];
if(simulator[i][3].equalsIgnoreCase("R"))
pointer++;
else if(simulator[i][3].equalsIgnoreCase("L"))
pointer--;
else if(simulator[i][3].equalsIgnoreCase("STOP"))
stop = true;
state = Integer.parseInt(simulator[i][4]);
break;
}
}
if(stop){
input = implode(tmp, "");
break;
}else{
input = implode(tmp, "");
System.out.println("Result = "+input + " AT state " + state + " looking at item = "+ pointer + " "+tmp[pointer]);
}
}
return input;
}
public String implode(String[] ary, String delim) {
String out = "";
for(int i=0; i<ary.length; i++) {
if(i!=0) { out += delim; }
out += ary[i];
}
return out;
}
The Universal turing machine takes in an input and a simulator in this case our simulator is an 2D array of instruction.
Simulator
My simulator is build in a 2D array of strings as mention previously. Here is an example of my simulator in an array.
String[][] Q1 = {
{"0", "_", "_","R", "0"},
}
And here is the explanation on what each column means.
- Current State
- Found Symbol
- Replace Symbol
- Move Direction (R - Right, L - Left)
- Move to State
Basically my simulator is that simple.
Multiplication Simulator
Now, i will provide you with my multiplication simulator with the following number of state required to calculate the multiplication of two numbers.
String[][] Q1 = {
{"0", "_", "_","R", "0"},
{"0", "1", "1","R", "0"},
{"0", "0", "_","R", "1"},
{"1", "0", "0","R", "1"},
{"1", "1", "0","L", "2"},
{"1", "_", "_","STOP", "2"},
{"2", "0", "0","L", "2"},
{"2", "_", "_","L", "3"},
{"3", "0", "0","L", "3"},
{"3", "_", "_","STOP", "3"},
{"3", "1", "0","R", "4"},
{"4", "0", "0","R", "4"},
{"4", "_", "_","R", "5"},
{"5", "0", "0","R", "5"},
{"5", "1", "1","R", "5"},
{"5", "_", "_1_","L", "6"},
{"6", "1", "1","L", "6"},
{"6", "0", "0","L", "6"},
{"6", "_", "_","L", "7"},
{"7", "0", "0","L", "7"},
{"7", "1", "0","R", "8"},
{"7", "_", "_","R", "10"},
{"8", "0", "0","R", "8"},
{"8", "_", "_","R", "9"},
{"9", "1", "1","R", "9"},
{"9", "0", "0","R", "9"},
{"9", "_", "_1","L", "6"},
{"10", "0", "1","R", "10"},
{"10", "_", "_","R", "11"},
{"11", "0", "0","R", "11"},
{"11", "1", "0","L", "13"},
{"11", "_", "_","STOP", "12"},
{"13", "0", "0","L", "13"},
{"13", "_", "_","L", "7"}
};
Well, you can see this takes 13 state to compute multiplication on a turing machine. The above doesn't make a sense to people who don't know what is a turing machine. It's like programming using your brain rather than a IDE editor when you are writing a simulator for a turing machine. Anyway, you can draw a diagram using the above instruction too. eg. input i placed in is "_1110111_". Calualte all the '1' on the right and stop when you see '_' to get your answer. 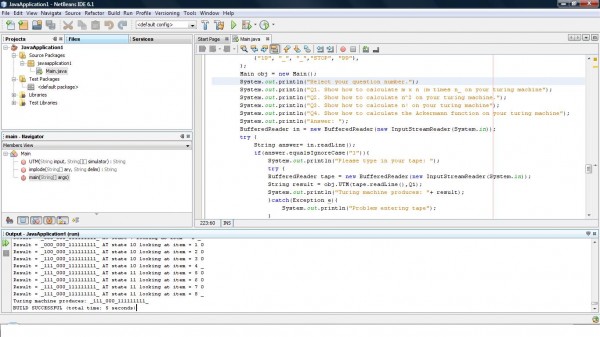
N x N Simulator
N x N simulator is fairly simple once you get multiplication to work. All you need to do is to clone the number into your input and perform a multiplication.
String[][] Q2 = {
{"0", "_", "_","R", "1"},
{"1", "0", "0","R", "1"},
{"1", "1", "0","R", "2"},
{"1", "_", "0","STOP", "99"},
{"2", "1", "1","R", "2"},
{"2", "_", "_","L", "3"},
{"3", "1", "10","R", "4"},
{"3", "0", "101","STOP", "99"},
{"3", "_", "_","STOP", "99"},
{"4", "0", "0","R", "4"},
{"4", "_", "1_","L", "5"},
{"5", "1", "1","L", "5"},
{"5", "0", "_","L", "6"},
{"6", "1", "1","L", "6"},
{"6", "0", "0","L", "6"},
{"6", "_", "_","R", "7"},
{"7", "0", "0","R", "7"},
{"7", "1", "0","R", "8"},
{"7", "_", "_","L", "10"},
{"8", "1", "1","R", "8"},
{"8", "_", "_1","L", "9"},
{"9", "1", "1","L", "9"},
{"9", "0", "0","L", "9"},
{"9", "_", "_","R", "7"},
{"10", "0", "1","L", "10"},
{"10", "_", "_","R", "11"},
{"11", "1", "1","R", "11"},
{"11", "0", "0","R", "11"},
{"11", "_", "0","STOP", "12"}
};
Above shows the simulator for duplicating your input from n to n x n. Once you have finish running this, run the multiplication simulator which will gives you a 24 state turing machine answer (11 + 13). eg. input i placed in is "_111_". Calualte all the '1' on the right and stop when you see '_' to get your answer. 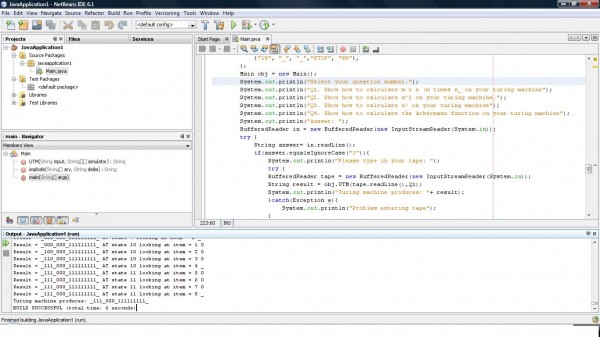
Factorial Simulator
Factorial can be modified from n x n. All you need to do is to modify the graph a little to get factorial answer. Please take note that my answer has not been optimized (i'm simply lazy to optimize for an assignment).
String[][] Q3 = {
{"0", "_", "_","R", "1"},
{"1", "0", "0","R", "1"},
{"1", "1", "0","R", "2"},
{"1", "_", "_","STOP", "99"},
{"2", "1", "1","R", "2"},
{"2", "_", "_","L", "3"},
{"3", "1", "10","R", "4"},
{"3", "0", "1","STOP", "99"},
{"3", "_", "_","STOP", "99"},
{"4", "0", "0","R", "4"},
{"4", "_", "1_","L", "5"},
{"5", "1", "1","L", "5"},
{"5", "0", "_","L", "6"},
{"6", "1", "1","L", "6"},
{"6", "0", "0","L", "6"},
{"6", "_", "_","R", "7"},
{"7", "0", "0","R", "7"},
{"7", "1", "0","R", "8"},
{"7", "_", "_","L", "10"},
{"8", "1", "1","R", "8"},
{"8", "_", "_1","L", "9"},
{"9", "1", "1","L", "9"},
{"9", "0", "0","L", "9"},
{"9", "_", "_","R", "7"},
{"10", "0", "1","L", "10"},
{"10", "_", "_","R", "11"},
{"11", "0", "0","R", "11"},
{"11", "1", "1","R", "11"},
{"11", "_", "0","R", "12"},
{"12", "1", "1","R", "12"},
{"12", "_", "_","L", "13"},
{"13", "1", "_","L", "14"},
{"14", "1", "1","L", "14"},
{"14", "0", "0","L", "14"},
{"14", "_", "_","R", "15"},
{"15", "1", "1","R", "15"},
{"15", "0", "_","R", "16"},
{"16", "0", "0","R", "16"},
{"16", "1", "0","L", "17"},
{"17", "0", "0","L", "17"},
{"17", "_", "_","L", "18"},
{"18", "0", "0","L", "18"},
{"18", "1", "0","R", "19"},
{"19", "0", "0","R", "19"},
{"19", "_", "_","R", "20"},
{"20", "0", "0","R", "20"},
{"20", "1", "1","R", "20"},
{"20", "_", "_1_","L", "21"},
{"21", "1", "1","L", "21"},
{"21", "0", "0","L", "21"},
{"21", "_", "_","L", "22"},
{"22", "0", "0","L", "22"},
{"22", "1", "0","R", "23"},
{"22", "_", "_","R", "25"},
{"23", "0", "0","R", "23"},
{"23", "_", "_","R", "24"},
{"24", "1", "1","R", "24"},
{"24", "0", "0","R", "24"},
{"24", "_", "_1","L", "21"},
{"25", "0", "1","R", "25"},
{"25", "_", "_","R", "26"},
{"26", "0", "0","R", "26"},
{"26", "1", "0","L", "27"},
{"26", "_", "_","L", "28"},
{"27", "0", "0","L", "27"},
{"27", "_", "_","L", "22"},
{"28", "0", "1", "R", "29"},
{"28", "1", "1", "L", "28"},
{"28", "_", "_", "R", "32"},
{"29", "1", "1", "R", "29"},
{"29", "_", "_", "R", "30"},
{"30", "1", "1", "R", "30"},
{"30", "_", "_1", "L", "31"},
{"31", "1", "1", "L", "31"},
{"31", "_", "_", "L", "28"},
{"32", "1", "1", "R", "32"},
{"32", "_", "_", "R", "33"},
{"33", "1", "1", "R", "33"},
{"33", "_", "_", "R", "34"},
{"34", "1", "1", "R", "34"},
{"34", "_", "_", "L", "35"},
{"35", "1", "_", "L", "36"},
{"36", "_", "_", "STOP", "36"},
{"36", "1", "1", "L", "37"},
{"35", "_", "_", "STOP", "35"},
{"37", "1", "1", "L", "37"},
{"37", "_", "0", "L", "38"},
{"38", "1", "1", "L", "38"},
{"38", "_", "_", "R", "15"},
};
It takes 38 state to compute factorial in my case but this can obviously to optimized (i saw many redundancy when i was writing this but i need to save time as its quite a last minute work before exam). All of these shouldn't be a problem as the logic is fairly simple. The real problem comes when ackerman function required you to recursive multiple sections. eg. input i placed in is "_111_". Calualte all the '1' on the right and stop when you see '_' to get your answer. 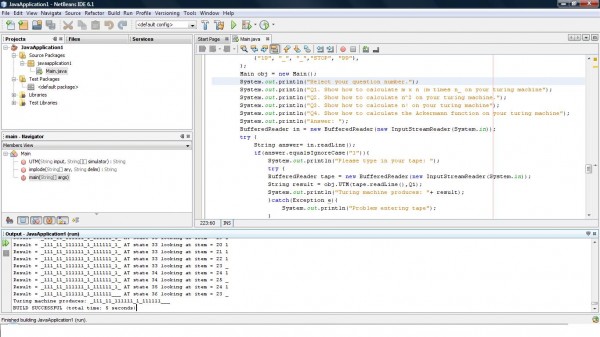
Ackerman Function Simulator
This is not fun but its rewarding if you manage to get the answer. Here is the simulator.
String[][] Q4 = {
{"0", "_", "_","R", "1"},
{"1", "0", "0","R", "2"},
{"1", "1", "1","R", "1"},
{"2", "1", "0","L", "3"},
{"2", "_", "_","L", "9"},
{"3", "0", "_","L", "4"},
{"4", "0", "0","L", "4"},
{"4", "1", "0","R", "5"},
{"4", "_", "_","R", "18"},
{"5", "0", "0","R", "5"},
{"5", "_", "_1","L", "6"},
{"6", "_", "_","R", "7"},
{"6", "1", "0","R", "5"},
{"6", "0", "0","L", "6"},
{"7", "_", "_","L", "8"},
{"7", "0", "1","R", "7"},
{"8", "1", "0","R", "0"},
{"9", "0", "1","L", "10"},
{"10", "1", "0","L", "11"},
{"10", "_", "_","STOP", "99"},
{"11", "_", "1","R", "13"},
{"11", "1", "1","L", "12"},
{"12", "1", "1","L", "12"},
{"12", "_", "_","R", "1"},
{"13", "1", "1","R", "13"},
{"13", "0", "1","R", "13"},
{"13", "_", "_","L", "14"},
{"14", "1", "_","L", "15"},
{"15", "1", "1","L", "15"},
{"15", "0", "0","L", "16"},
{"16", "_", "1","R", "17"},
{"16", "1", "1","L", "12"},
{"17", "1", "1","R", "17"},
{"17", "0", "1","R", "17"},
{"17", "_", "_","L", "14"},
{"18", "_", "1","R", "19"},
{"19", "0", "1","R", "19"},
{"19", "1", "1","R", "19"},
{"19", "_", "_","STOP", "99"},
};
I manage to create an ackerman function with a 19 state while you might need to create 50-100 state to perfect an ackerman function (my classman has 120+ state). Anyway, this ackerman function IS buggy but it should be good enough to give you some hints or an idea after you have drawn the diagram of this simulator. You will find that this ackerman function ends with a missing starting symbol! Short to say, the turing machine ends when it hits an empty string while replacing the starting symbol as a value. I will show you rather than explaining. eg. input i placed in is "_11011_". Calualte all the '1' to get your answer. 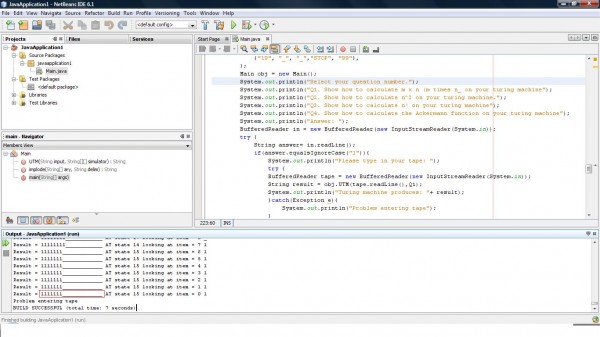 Do take note of the highlighted answer. The total seems correct but it actually violated the term 'turing machine' as it didn't stop at the halt state but stop due to the exception of access an empty index on the string array (-1 in this case). Hehe, good luck.
Do take note of the highlighted answer. The total seems correct but it actually violated the term 'turing machine' as it didn't stop at the halt state but stop due to the exception of access an empty index on the string array (-1 in this case). Hehe, good luck.
Input
Here is the explanation of my input.
- "_" - this is the start and end point
- "0" - this is the multiplication symbol (its not always the case when its IN the simulator, i'm talking about the input here 🙂
- "1" - this is the value
pretty simple and i keep the same rule for the whole 4 question. All the answer can be found on the right side or left with the number '1'.
Java Code
here is the source code of the whole thing.
Conclusion
The material above is use to serve as a reference for your work. It serves as a starting point on "how to do?" question.


